[最も人気のある！] x(1-x^2)dy/dx (2x^2-1)y=ax^3 103425

 Solve the following differential equation (x3x2x1)dy/dx=2x2x Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesF' (x) = a n xn1 y = ex dy/dx = ex y = ea x dy/dx = a ea x y = ax dy/dx = ax ln (a) y = ln (x) dy/dx = 1 / xIntegrate 1/(cos(x)2) from 0 to 2pi;

X 1 Y 2 Dx Y 1 X 2 Dy 0 Youtube

X(1-x^2)dy/dx (2x^2-1)y=ax^3

X(1-x^2)dy/dx (2x^2-1)y=ax^3-2x d (y 2)×dy = 3 dy dx 2x 2y dy = 3 dx dy = 3 2x dx 2y Example Differentiate a x with respect to x You might be tempted to write xa x1 as the answer This is wrong That would be the answer if we were differentiating with respect to a not x Put y = a xSimple and best practice solution for (x2y4)dx(2xy5)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework

First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download

Encontrar la solución implícita de la siguiente ecuación diferencial dy(xy 2x 4y 8) dx(xy 3x y 3) = 0 dy xy 3x y 3 = dx xy 2x 4y 8 dy x(y 3) (y 3) = dx x(y 2) 4(y 2) dy (y 3)(x 1) = = f ( y )g ( x );If y 2 = ax 2 bx c, where a, b and c are constant, then y 3 d 2 y/dx 2 is Leave a Comment Cancel reply Your Mobile number and Email id will not be publishedUse implicit differentiation to find dy/dx for question x^2y^2=1 asked in CALCULUS by angel12 Scholar implicitdifferntiation;

(x 2 − y 2) d y d x = 2 x y d y d x = 2 x y x 2 − y 2 = 2 (y / x) 1 − (y / x) 2 The trick in this case should be pretty obvious Set v = y x Therefore, y = x vDy dx = (x 2)(y 1) (x 3)(y 1) 2 Separating the variables leads to y 1 y 1 dy = x 2 x 3 dx 3 To evaluate the integrals Z y 1 y 1 dy = Z x 2 x 3 dx we need usubstitution on both sides On the LHS, let u = y 1 and then du = dy and y = u1 On the RHS we need another variable name, so let w = x 3 and then dw = dx and x = w 3 Substituting (01 below),386 Chapter 15 Multiple Integration c y 1 y 2 y 3 d a x 1 x 2 x 3 x 4 x 5 b ∆x ∆y Figure 1511 A rectangular subdivision of a,b×c,d Using sigma notation, we can rewrite the approximation 1 mn

Laminiaduo7 and more users found this answer helpfulFind dy/dx x^2yy^2x=2 Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps By the Sum Rule, the derivative of with respect to is Evaluate Tap for more steps Differentiate using the Product Rule which states that is where and To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(1x^2)dy/dx2xy=(x^22)(x^21)`

Verifying Solutions To Differential Equations Video Khan Academy

Ex 9 6 8 Find General Solution 1 X2 Dy 2xy Dx Ex 9 6

Solve (cosx tany cos(xy))dx (sin x sec 2 ycosV dv/dx = v v^3/2 Simplify;Since the sum of the exponents of x and y is the same in every term, the substitution y = vx, where v is a function of x, will work y = vx => y'= v xv' Substitute in the given equation and divide by 2x^3;

If Y X Is The Solution Of Dy Dx X 2 1 Y 2 Y 0 2 Then Y 3 Homeworklib

Engineering Mathematics Notes

 Ex 95, 15 For each of the differential equations in Exercises from 11 to 15 , find the particular solution satisfying the given condition 2𝑥𝑦𝑦^2−2𝑥^2 𝑑𝑦/𝑑𝑥=0;𝑦=2 When 𝑥=1 Differential equation can be written 𝑎s 2𝑥𝑦𝑦^2−2𝑥^2 𝑑𝑦/𝑑𝑥=0 2𝑥𝑦𝑦^2= 2𝑥^2 𝑑𝑦/𝑑𝑥 2𝑥^2 𝑑𝑦/𝑑𝑥=2𝑥𝑦𝑦^2 𝑑𝑦/Let's simplify it First dy/dx = (y/x 1)/(y/x 1) Taking y = vx dy/dx = v xdv/dx Therefore, dx/x = (v 1)dv / (v^2 1) Integrating we get log (1/x) logc = arctan (y/x) 1/2 logSolve The Differential Equation We are given a firstorder differential equation of the form {eq}P \ dx Q \ dy = 0 {/eq} Integration and differentiation are related to each other

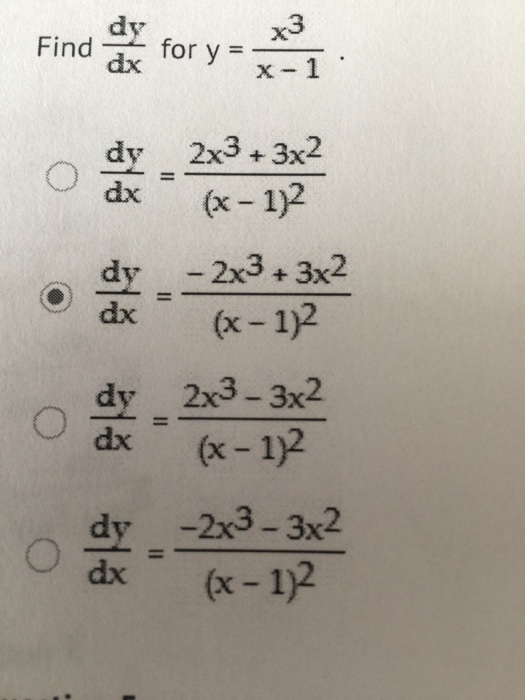
Solved Find Dy Dx For Y X 3 X 1 Dy Dx 2x 3 3x 2 Chegg Com

X 1 Y 2 Dx Y 1 X 2 Dy 0 Youtube

Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;Integrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity; The solution of x^3(dy/dx) 4x^2 ∙ tany = e^x ∙ secy satisfying y(1) = 0 is asked in Mathematics by Ankitk ( 742k points) differential equations

Differential Equations

Differential Equations Ppt Download

 Ex 53, 1 Find 𝑑𝑦/𝑑𝑥 in, 2𝑥 3𝑦 = sin⁡𝑥 Given 2𝑥3𝑦 = sin⁡𝑥 Differentiating both sides 𝑤𝑟𝑡𝑥 (𝑑 (2𝑥 3𝑦Sec2 y dy dx 1 2 √ 1x tany = 1 √ 19 Exact Differential Equations For the next technique it is best to consider firstorder differential equations written in differential form M(x,y)dxN(x,y)dy= 0, (191) where M and N are given functions, assumed to be sufficiently smooth8 The methodDx (y 2)(x 4) (y − 2 )dy (x − 1)dx = ⇒ Integramos a ambos lados de la ecuación (y 3

The Differential Equations X 3 X 2 X 1 Dy Dx 2x 2 X Y 1 Sarthaks Econnect Largest Online Education Community

How To Get The Special Solution Of This Differential Equation Y Xdy Dx 2 1 X 2 Dy Dx Where X 1 Y 1 Quora

View more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator Learn3 Finding Z f(g(x))g′(x)dx by substituting u = g(x) Example Suppose now we wish to find the integral Z 2x √ 1x2 dx (3) In this example we make the substitution u = 1x2, in order to simplify the squareroot term We shall see that the rest of the integrand, 2xdx, will be taken care of automatically in the2dv/v^3 = dx This can be easily solved to obtain v and then y = vx 4 views

First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download

Solve X 1 X 2 Dy 2x 2y Y Ax 3 Dx 0

Start with y = sin−1 (x) In non−inverse mode x = sin (y) Derivative d dx (x) = d dx sin (y) 1 = cos (y) dy dx Put dy dx on left dy dx = 1 cos (y) We can also go one step further using the Pythagorean identity sin 2 y cos 2 y = 1 cos y = √ (1 − sin 2 y ) And, because sin (y) = x (from above!), we getFree separable differential equations calculator solve separable differential equations stepbystepSimple and best practice solution for (2x3y4)dx3(x1)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it

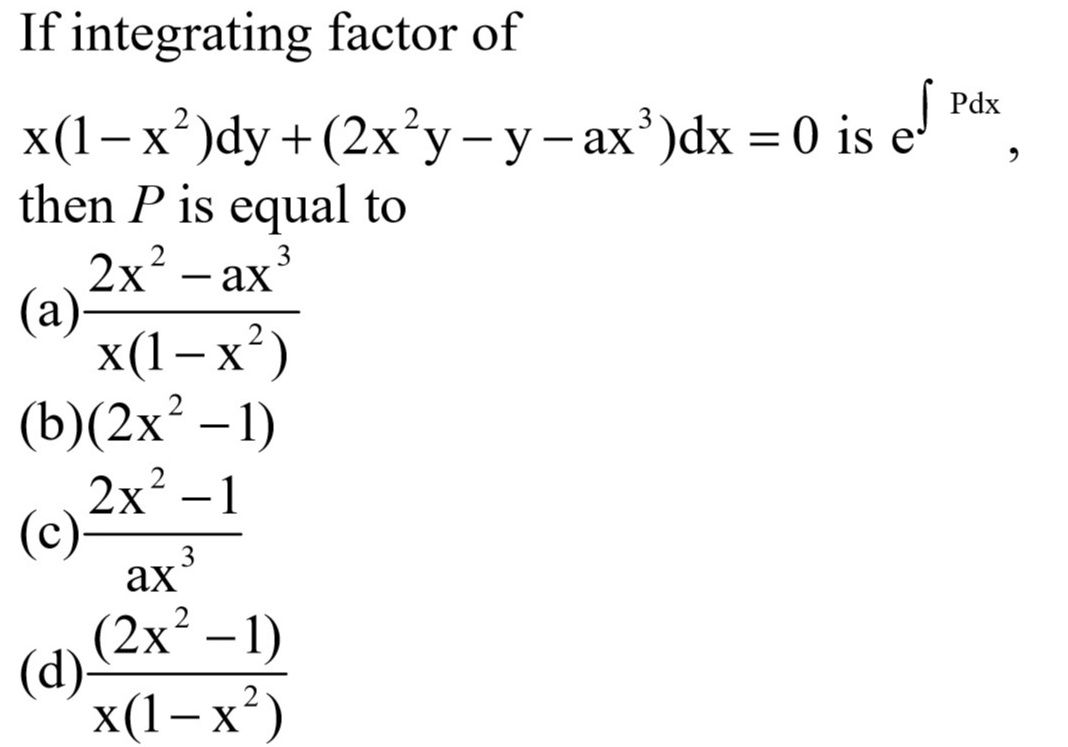
Find The Cartesian Equation Of The Curves Given By These Parametric Equations X 4t Y 2t 2 Snapsolve

Solved Solve Each Differential Equation Dy Dx 5y E 3x Chegg Com

Example 1 Solve the differential equation dy / dx 2 x y = x Solution to Example 1 Comparing the given differential equation with the general first order differential equation, we have P(x) = 2 x and Q(x) = x Let us now find the integrating factor u(x) u(x) = e ò P(x) dx = e ò2 x dx = e x 2 We now substitute u(x)= e x 2 and Q(x) = x in the equation u(x) y = ò u(x) Q(x) dx to obtain1For each part, nd dy=dx (a) y= 3x3 2x2 p x Answer dy dx = 15 2 x3=2 3x1=2 (b) y= xe2x Answer dy dx = (2x 1)e2x (c) y= 1 2 sin( 2x) Answer dy dx = cos( 2x) (d) xy= x2 y2 Answer dy dx = 2x y x 2y (e) y= Z x 3 e t2 dt Answer dy dx = e x2 (f) y= ( 5x 2)4 Answer dy dx = 3( 5x 2) (g) y= R 2 x 3sin(t2)dt Answer 3sin(x2) (h) d dxExample 1 d 2 ydx 2 − y = 2x 2 − x − 3 (For the moment trust me regarding these solutions) The homogeneous equation d 2 ydx 2 − y = 0 has a general solution y = Ae x Bex The nonhomogeneous equation d 2 ydx 2 − y = 2x 2 − x − 3 has a particular solution y = −2x 2 x − 1 So the complete solution of the differential equation is

If Integrating Factor Of X 1 X 2 Dy 2x 2y Y Ax 3 Dx 0 Is E Pdx Then P Is Equal To Sarthaks Econnect Largest Online Education Community

Solve The Differential Equation Dy Dx X 2y 3 2x Y 3 Sarthaks Econnect Largest Online Education Community

Ejercicios EDO's de primer orden 3 1 y3 dy = dx x2 Z y−3 dy = Z x−2 dx, 1 −2 y−2 = −x−1 c 1, −1 2y2 −1 x c 1, 1 y2 2 x c, c = −2c 1 Solución implícita 1 y2 2xc x Solución explícita y = ±Popular Problems Calculus Find dy/dx 2xyy^2=1 2xy − y2 = 1 2 x y y 2 = 1 Differentiate both sides of the equation d dx (2xy−y2) = d dx (1) d d x ( 2 x y y 2) = d d x ( 1) Differentiate the left side of the equation Tap for more steps By the Sum Rule, the derivative of 2 x y − y 2 2 x y y 2 with respect to x x is d d x 2Aprende en línea a resolver problemas de ecuaciones diferenciales paso a paso Resolver la ecuación diferencial dy/dx=(x1)^2 Agrupar los términos de la ecuación diferencial Mover los términos de la variable y al lado izquierdo, y los términos de la variable x al lado derecho de la igualdad Simplificar la expresión \left(x1\right)^2dx

Differential Equation

Engineering Mathematics Notes

 Find dy/dx for the equation x^32x^2y3xy^2=38 asked in CALCULUS by andrew Scholar derivatives;Linear in y dy dx − 2 x y = x3 sinx Integrating factor IF = e −2 R dx x = e 2ln x = eln x −2 = 1 x2 Multiply equation 1 x2 dy dx − 2 x3 y = xsinx ie d dx 1 x2 y = xsinx Integrate y x2 = −xcosx− Z 1·(−cosx)dxC0 Note integration by parts, R udv dx dx = uv − R vdu dx dx, u = x, dv dx = sinx ie y x2 = −xcosxsinxC i Help a stranger please This is for my homework and I'm having a hard time solving these equations Show the complete solutions and final answers please It will be a great help Thank you so much This covers Additional Topics on Equations of Order One, Coefficient Linear in Two Variables 1 (6x3y2)dx(2xy1)dy=0 2 (x2y1)dx(2xy5)dy=0

Solution Of X Y 2 Dy Dx A 2 A Being A Constant Is Youtube

Differential Equations Separation Of Variables Ppt Download

 Substitute y = t x t ( t 2 x) = ( t − 2 x) y ′ Note that y ′ = t ′ x t t ( t 2 x) = ( t − 2 x) ( t ′ x t) After some simplifications you get t ′ ( t − 2 x) = 4 t Consider now x ′ = d x d t x ′ x 2 t = 1 4 Which is easy to solveClick here👆to get an answer to your question ️ solve x(1x^2)dy (2x^2y y ax^3)dx = 0Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance

Differential Equations Separation Of Variables Ppt Download

How To Find Dy Dx Of The Function Y X 1 X 2 X 1 2 Quora

Section 3 Answers 7 3 Answers 1 y = Ax, 2 y2x−x2 = A, 3 (y 1)ex −y2 = A, 4 x2y 3x2 y4 = A, 5 1 2 x 2(1−y )4y2 = A, 6 1 4 e 4x x2y2 siny = A, 7 x3 ysinx−y4 = A, 8 x2 2 tan −1 y = A, 9 x2 x3y3 3 y 4 = A, Toc JJ II J I Back x^2xyc =intdy=int2xydx =y=(2x^2)/2xyc =y=x^2xyc Hope it helps!Most Used Actions \mathrm {implicit\derivative} \mathrm {tangent} \mathrm {volume} \mathrm {laplace} \mathrm {fourier} See All area asymptotes critical points derivative domain eigenvalues eigenvectors expand extreme points factor implicit derivative inflection points intercepts inverse laplace inverse laplace partial fractions range slope

Find The General Solution Of Differential Equation X 2 Y 1 Dx Y 2 X 1 Dy 0 Sarthaks Econnect Largest Online Education Community

1

(2) Let y 1 (x) and y 2 (x) be any two solutions of the homogeneous equation, then any linear combination of them (ie, c 1 y 1 c 2 y 2) is also a solution (3) The general solution of the differential equation is given by the linear combination y(x) = c 1 y 1 (x) c 2 y 2 (x) where c 1 and c 2 are arbitrary constants, and y 1 (x) and y 2Xe ax2 dx= 1 2a e 2 (70) Z x2e ax2 dx= 1 4 r ˇ a3 erf(x p a) x 2a e ax2 Integrals with Trigonometric Functions (71) Z sinaxdx= 1 a cosax (72) Z sin2 axdx= x 2 sin2ax 4a (73) Z sin3 axdx= 3cosax 4a cos3ax 12a (74) Z sinn axdx= 1 a cosax 2F 1 1 2;3 2;cos2 ax (75) Z cosaxdx= 1 a sinax (76) Z cos2 axdx= x 2 sin2ax 4a (77) Z cos3 axdx

Solve X D 2 Dx 2 2x 1 Dy Dx X 1 Y 0 Given That Y E X Is An Integral Included In The Complementary Function सम करण X D 2 Dx 2 2x 1 Dy Dx X 1 Y 0 क हल क ज ए द य गय ह क Y E X

What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora

Rewriting the given diff eqn (DE) as #dy/dxy=2x#, we find that it is a linear DE of the form #dy/dxyP(x)=q(x)# To find its gen soln (GS), we need to multiply it by the integrating factor (IF) #e^(intP(x)dx# Since,Find dy/dx given x^3 3 x^2 y 2 x y^2 = 12 Natural Language; dy dx = 2x (y x2y)2 this is separable dy dx = 1 y2 ⋅ 2x (1 x2)2 y2 dy dx = 2x (1 x2)2 ⇒ y3 3 = − 1 1 x2 C y3 = C − 3 1 x2 y = 3√C − 3 1 x2

Solved Solve The Initial Value Problems A X 2 Dy Dx 4x 2 Chegg Com

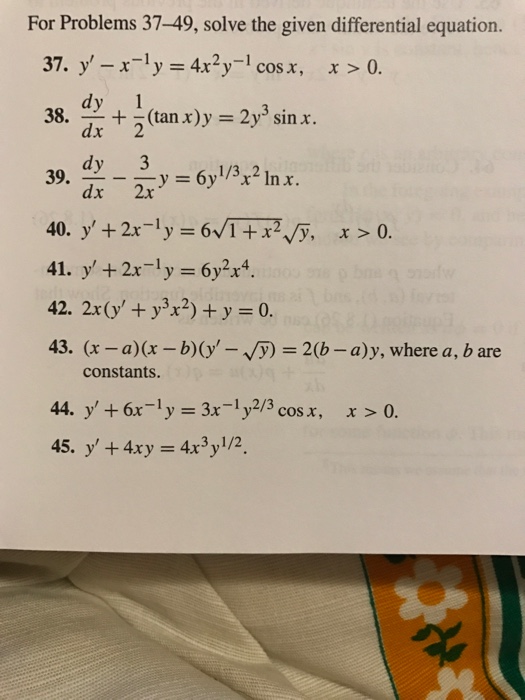
Solved Solve The Given Differential Equation Y X 1 Y Chegg Com

Eg1 Write input √x as x^(1/2) 2 Write 5x as 5*x 3 Write x5 as x5 4 Write x 25x as x^25*x 3 Use paranthesis() while performing arithmetic operations Eg1 Write sinxcosxtanx as sin(x)cos(x)tan(x) 2 Write secx*tanx as sec(x)*tan(x) 3 Write tanx/sinx as tan(x)/sin(x) 4 Use inv to specify inverse and ln to specify natural log So, dy/dx = 2x 1 After performing Long division, We get it Or y = (x^4x^21)/ (x^2x1) y = ( x^2 x 1 ) ( x^2 x 1 ) / x^2 x 1 y = x^2 x 1 dy/dx = 2x 1 Hope helped! 2 回答 dy/dx＝y^2－1 を解いてください dy/dx－ (x＋y)^2 ＝0 一般解が知りたいです (d^4 y)/dx^4 －2 (d^2 y)/dx^2 ＝0 これができたらすごい dy/dx＝y^2－1 を解いてください dy/dx－ (x＋y)^2 ＝0 一般解が知りたいです (d^4 y)/dx^4 －2 (d^2 y)/dx^2 ＝0 これができたらすごい コイン

Solve X D 2 Dx 2 2x 1 Dy Dx X 1 Y 0 Given That Y E X Is An Integral Included In The Complementary Function सम करण X D 2 Dx 2 2x 1 Dy Dx X 1 Y 0 क हल क ज ए द य गय ह क Y E X

What Is The Solution Of The Differential Equation Dy Dx 1 E X Y Quora

\frac{dy}{dx}=1x^2y^2, Given Here, \frac{dy}{dx} represents the derivative of y with respect to x I will solve for x and y, treating y as a function of x (essentially y=f(x)) \int \frac{dy}{dx}dx=\int 1x^2y^2dxI am solving this linear Differential equation which can be easily solve by using the formulas for the Bernoulli's Equations I have solved till $$\frac{dy}{dx}\frac{(2x^21)y^3}{3x(1x^2)y^2}=\f

Solve X X 1 Dy Dx X 2 Y X 3 2x 1 Sarthaks Econnect Largest Online Education Community

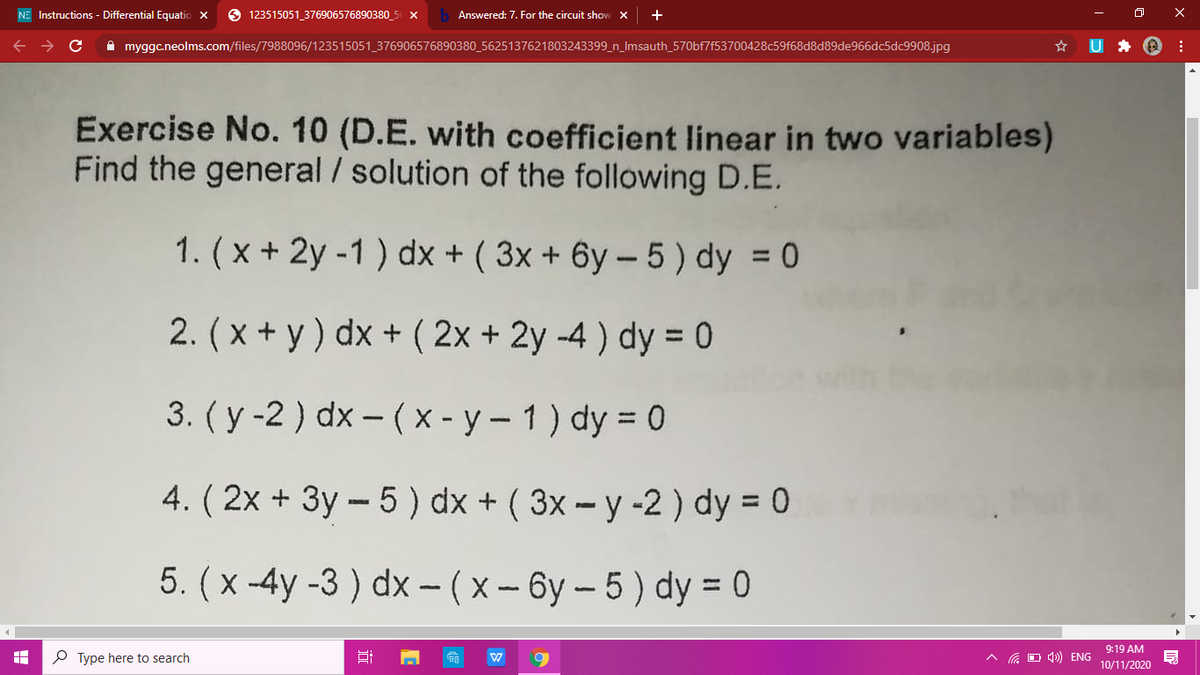
Answered 4 2x 3y 5 Dx 3x Y 2 Dy Bartleby

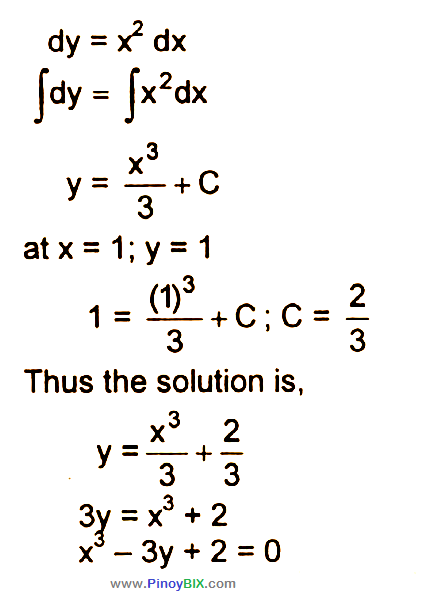
Solution If Dy X 2 Dx What Is The Equation Of Y In Terms Of

How Do I Solve The Following Differential Equation Math X 1 X 2 Dy Over Dx 2x 2 1 Y X 3 Math Quora

If Y X Is The Solution Of Dy Dx X 2 1 Y 2 Y 0 2 Then Y 3 Homeworklib

Solve The Differential Equation X 1 Dydx 2x 3y

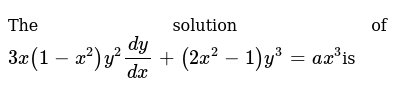
The Solution Of 3x 1 X 2 Y 2dy Dx 2x 2 1 Y 3 A X 3is

The Solution Of 3x 1 X 2 Y 2dy Dx 2x 2 1 Y 3 A X 3is

1

Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com

X X 3 Dy Dx 2x 2 1 Y A X 3

Example 9 Find General Solution Of Dy Dx X 1 2 Y Examples

Solved Solve The Differential Equation X 2 Dy Dx X Chegg Com

Solved I 2x Y 1 Dx Ydy 0 Ii Xydx X2 Y2 Dy 0 Chegg Com

2

What Is The General Solution Of The Differential Equation 2x 2y 3 Dy Dx X Y 1 Quora

How To Homogeneous Reducible Differential Equation Dy Dx 2x Y 1 X 2y 1 Quora

Differential Equatio Long Answer Questions 7 M R Solye 2x Y 3 Dx 2y X 1 Dy Sol Dy 2x Y 3 Given Equation Is

How To Solve The Differential Equation Dy Dx X Y 1 2x 2y 3 Quora

X 2 Y 2 Dy Dx Xy Solve The Above Equation

Misc 14 Find Particular Solution X 1 Dy Dx 2e Y 1

Differential Equations Separation Of Variables Ppt Download

Dy Dx 3x 2 1 Y 2 3 2 Socratic

Basic Differentiation Tutorial For Igcse And A Level Maths Vivax Solutions

Engineering Mathematics Notes

Exact Equations Example 3 Video Khan Academy

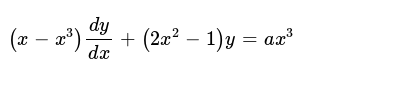
X X 3 Dy Dx 2x 2 1 Y A X 3

Solve X X 1 Dy Dx Y X2 X 1 2 Maths Differential Equations Meritnation Com

Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange

Solve X 1 X 2 Dy Dx 2x 2 1 Y Ax 3 Youtube

If Y X X2 1 1 2 M Then Show That X2 1 D2y Dx2 X Dy Dx M2y 0 Mathematics Topperlearning Com 6jd9kell

Solved Solve X 1 X 2 Dy 2x 2y Y Ax 3 Dx 0

Engineering Mathematics Notes

If 1 X 2 1 Y 2 A X Y Then Prove That Dy Dx

Solved Solve The Following Differential Equations X Y 3 Dx X Y 1 Dy 0 2 X Y 1 Dx 3x 4y 2 Dy C 3 1 Y 2 Xy 2 Dx X 2y Y 2xy Dy Course Hero

Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange

Solve X 2 D 2y Dx 2 X Dy Dx Y 0 Given That Y X 1 X Is A Solution Of It Youtube

Solved Bernoulli S Equation 6y 2 Dx X 2x 3 Y Dy 0 Chegg Com

Implicit Differentiation

Solve The Differential Equation X2 1 Dy Dx 2xy 1 X2 1 Studyrankersonline

For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The Following Are True Youtube

Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange

ベストコレクション Y X 2 1 X 2 Find Dy Dx Y Log 1 X 2 1 X 2 Find Dy Dx Sikatbabat8yjl

X 1 Y Y 1 X 0 Dy Dx K X 1 2 Mathematics Topperlearning Com

Homogeneous Differential Equations

Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange

Mathematics Ii Tranquileducation

Solving The Bernoulli Differential Equation X 2 Dy Dx Y 2 Xy Youtube

Can Anyone Solve This 2x 3y 1 Dx 3x 2y 1 Dy 0 Quora

0以上 Y X 2 2x 1 X 3 Y X 2 2x 8 Y 0 X 1 X 3 Duongmopintjos

2

Ex 9 4 12 Find Particular Solution X X2 1 Dy Dx 1 Y 0

Engineering Mathematics Notes

How To Get The Special Solution Of This Differential Equation Y Xdy Dx 2 1 X 2 Dy Dx Where X 1 Y 1 Quora

X X 3 Dy Dx 2x 2 1 Y A X 3

1 X 2 Dy Dx Xy 1 Youtube

Separable Equations Example Old Video Khan Academy

Ex 9 4 11 Find Particular Solution X3 X2 X 1 Dy Dx

Chapter 1 1st Order Linear Differential Equations

Worked Example Identifying Separable Equations Video Khan Academy

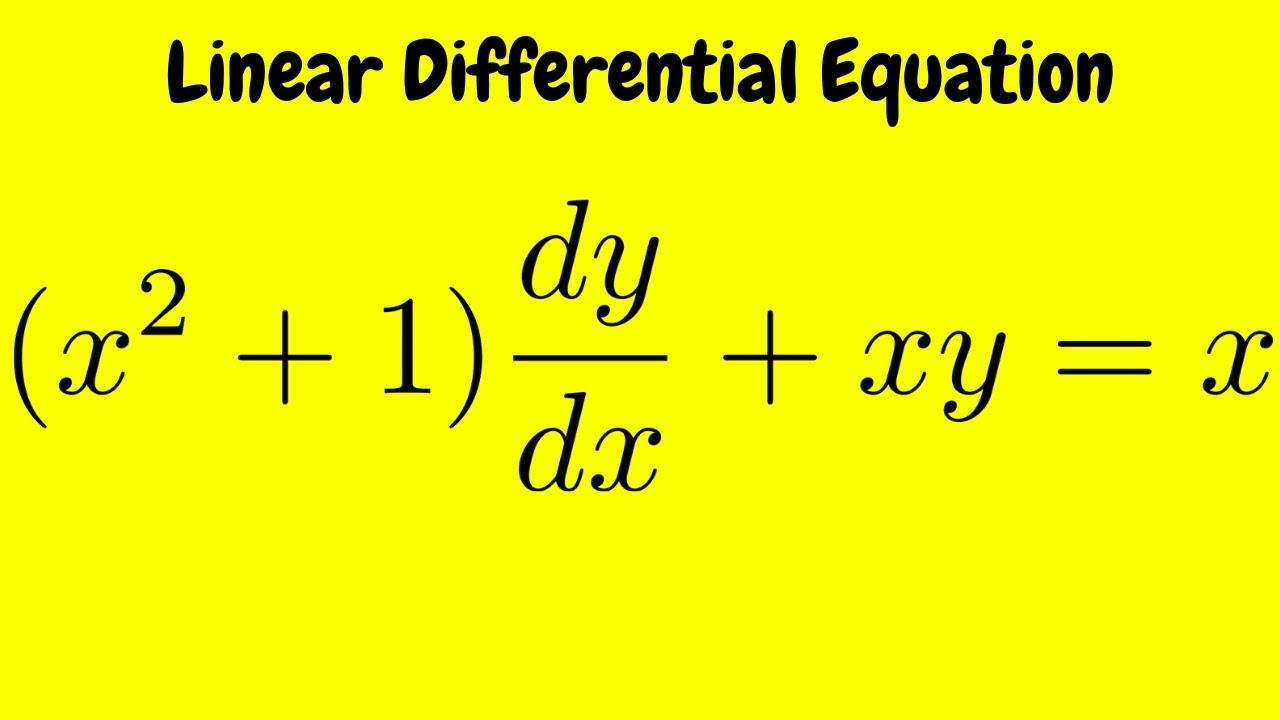
Solve The Linear Differential Equation X 2 1 Dy Dx Xy X Youtube

Solve The Differential Equation X 1 X 2 Dy 2x 2y Y 5x 3 Dx 0 Sarthaks Econnect Largest Online Education Community

Ex 9 4 11 Find Particular Solution X3 X2 X 1 Dy Dx

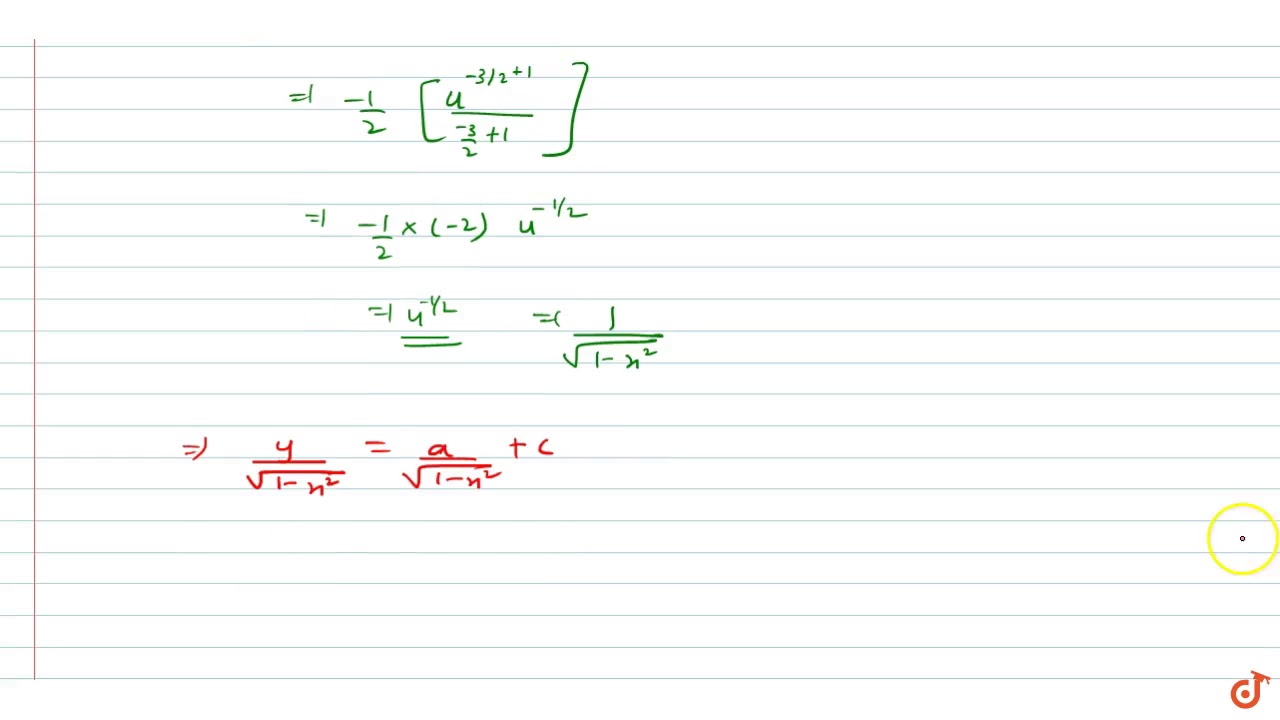
Solutions Of The Differential Equation 1 X 2 Dy Dx Xy Ax Where A In R Is Youtube

2

X X 3 Dy Dx 2x 2 1 Y A X 3

Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy

Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection

Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When

Solve X X 1 Dy Dx X 2 Y X3 2x 1 Maths Application Of Derivatives Meritnation Com

Engineering Mathematics Notes

X 1 X 2 Dy 2x 2y Y Ax 3 Dx 0

How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic

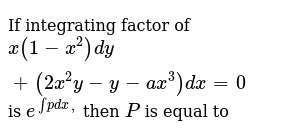
If Integrating Factor Of X 1 X 2 Dy 2x 2y Y A X 3 Dx 0 Is E Intp Dx Then P Is Equal To